Математическая модель оптимизации организационных процессов предприятия с дискретным производством

ВВЕДЕНИЕ

Большинство проблем в изучаемой области связано с потребностью в инструментах, поддерживающих принятие решений о размещении новых промышленных объектов и управлении уже существующими [1]. Необходимость в подобных инструментах возникает в отношении производственных предприятий, складов, центров снабжения, когда встает вопрос об их реструктуризации, перемещении либо окончательной ликвидации.

Наиболее типичной является логистическая проблема, когда необходимо одновременно разместить два или более объекта или добавить объект, когда хотя бы один объект уже существует [2]. В случае, когда объектов больше, количество возможных конфигураций становится огромным и ситуация труднообозримой [3].

Существует множество проблем, присущих цепочкам поставок, не разработанных должным образом каждым из участников цепочки [4]. Большинство из них возникают из-за неудачного расположения промышленного объекта, что может повлиять на другие области планирования цепочки, такие как политика инвентаризации или транспортировка продукции. Об этой ситуации свидетельствует чрезмерное использование запасов, увеличение затрат на логистику, увеличение долгосрочных капитальных вложений и снижение уровня обслуживания клиентов [5].

Цепочка поставок объединяет производственную цепочку поставщика, производства, транспортировки, хранения, распределения и конечного потребителя. Направление цепочки поставок отвечает за синхронизацию требований потребителя с потоком материалов поставщиков, это для того, чтобы получить баланс, который отражается в вопросах снижения удельных затрат, снижения запасов, сокращения возвратов и отказов, чтобы улучшить обслуживание клиентов и повысить гибкость (объем доставки) [6, 7]. Цепочки поставок включают в себя множество звеньев, и их конкретный состав зависит от отрасли, продукта и стратегии компании. Можно выделить несколько основных звеньев, которые чаще всего присутствуют:

Поставщики сырья и материалов – начальное звено, обеспечивающее исходные материалы для производства. Это могут быть как производители сырья (например, рудники для добычи металлов), так и поставщики готовых компонентов (например, производители микросхем для электроники).

Производители преобразуют сырье и материалы в готовые продукты или промежуточные товары. Это может быть как собственное производство компании, так и привлечение сторонних производителей (outsourcing).

Поставщики компонентов и запчастей: даже если компания сама производит основной продукт, ей часто нужны компоненты и запчасти от других поставщиков.

Склады и логистические центры: здесь происходит хранение и управление запасами, а также сортировка и подготовка товаров к дальнейшей доставке.

Транспортные компании отвечают за физическую доставку товаров на всех этапах цепочки поставок – от поставщиков сырья до конечных потребителей. Это включает в себя различные виды транспорта: автомобильный, железнодорожный, морской, воздушный.

Дистрибьюторы и оптовики закупают товары у производителей оптом и перепродают их розничным продавцам.

Розничные продавцы – конечное звено, которое продает товары непосредственно потребителям. Это могут быть как физические магазины, так и онлайн-платформы.

Потребители (клиенты) – конечные пользователи товаров и услуг.

Дополнительные звенья (в зависимости от контекста): сервисные компании (предоставляют услуги, связанные с обслуживанием, ремонтом и утилизацией товаров); финансовые учреждения (обеспечивают финансирование на разных этапах цепочки поставок); таможенные органы (осуществляют контроль за перемещением товаров через границы); регуляторные органы (устанавливают стандарты и правила, касающиеся безопасности, качества и экологических аспектов); информационные и технологические компании (предоставляют программное обеспечение и другие технологии, необходимые для управления цепочкой поставок).

Основная цель цепочек поставок – удовлетворить клиента и в процессе этого получить прибыль, т. е. максимизировать общую созданную стоимость. Прибыль, создаваемая цепочкой поставок, представляет собой разницу между стоимостью конечного продукта для покупателя и затратами на выполнение запроса клиента [8][9].

Основные элементы цепочки поставок – это: продукты (в переработке, транспортировке, хранении); потребители или клиенты; провайдеры; производственные предприятия; дистрибьюторские центры; оптовые дистрибьюторы; розничные торговцы или оптовые торговцы; логистические операторы; транспортные системы или виды транспорта; информационные системы; зеленая логистика и т. д. [10].

Информационные системы цепочки поставок являются предметом исследования для многих авторов [11][12]. Существует несколько интегрированных информационных систем, таких как SAP и ORACLE, называемых ERP (Планирование ресурсов предприятия), которые предоставляют и интегрируют информацию по всей цепочке поставок через ключевые модули, такие как закупки и поставщики, финансовый и бухгалтерский учет, человеческие ресурсы, планирование производства, планирование транспортировки и операции (Системы управления транспортом ТМС), системы управления складом (Системы управления складом WMS), модули прогнозов и запасов, модуль управления связями с клиентами (Управление взаимоотношениями с клиентами CRM), среди прочих возможных.

К типичным операциям относятся [13–15]: администрирование портфеля продуктов и услуг, контроль производства, кейтеринг, распределение. Чтобы понять, как компания может повысить производительность цепочки поставок с точки зрения оперативности и эффективности, необходимо изучить движущие силы поведения компании: объекты, запасы, распределение, информация, закупки и ценообразование [16]. Для успешного управления цепочкой поставок требуются решения, связанные с потоком информации, продуктов и средств [17–20].

Математическое моделирование как инструмент оптимизации управления предприятием. Методы оптимизации есть адекватный инструмент для проектирования сети, в котором при принятии решения важно учитывать многие логистические аспекты, связанные с количеством, расположением и размером складов в логистической сети [21][22]. Задачи оптимизации возникают, когда необходимо принять решение о том, чтобы оптимальным образом распределить ограниченные ресурсы на действия, которые конкурируют друг с другом за них, для достижения наилучших результатов [23].

При оптимизации цепочек поставок обычно применяется линейное программирование [24]. В случае, когда вся цепочка еще не существует и, например, определяется новое местоположение завода или одного или нескольких распределительных центров, генерируются целочисленно-смешанные задачи линейной оптимизации [25].

В источнике [26] разработано математическое моделирование детерминистического производства и распределения, применяемое к компании по поставкам медицинских товаров для оптимизации всей цепочки поставок. Как отмечает Шапиро [27]: «Модели оптимизации являются необходимыми и желательными инструментами для определения эффективных решений в цепочке поставок. Это единственные инструменты, способные комплексно анализировать сложные взаимодействия решений, принимаемых по всей цепочке поставок компании».

Это свидетельствует о том, что линейное программирование является важным аспектом создания оптимизационных моделей. Математические концепции должны быть развиты и адаптированы к бизнес-теме таким образом, чтобы они позволяли экономить время и проводить анализ различных сценариев с целью принятия решений с минимальной вероятностью ошибки.

Этапы проектирования математической модели следующие [13][28–32]: 1) определение интересующей проблемы и сбор соответствующих данных; 2) формулировка математической модели, которая представляет проблему; 3) разработка процедуры на основе программного обеспечения для получения решения проблемы из модели; 4) анализ результатов.

Цель настоящего исследования – математическое моделирование организационных процессов предприятия с дискретным производством, направленного на их оптимизацию и использующего как инструмент линейное программирование, а также числовые ряды данных, всесторонне характеризующие работу предприятия в течение заданного года.

Объект моделирования – производственная цепочка предприятия дискретного типа, включающая производство, транспортировку, хранение, распределение и доставку продукции потребителям.

Предмет моделирования – производственная цепочка предприятия Ростовской области по производству снеков, имеющего два завода – в Морозовске и Константиновске – и поставляющего свою продукцию в 11 районов области.

Задачи моделирования:

– анализ ситуации на предприятии, сбор данных, выявление определяющих условий работы предприятия, оптимизируемых параметров и производственных ограничений;

– разработка математической модели предприятия на основе задачи линейного программирования, математическая формализация требований к производству и логистике предприятия;

– реализация модели на основе генератора AMPL (язык моделирования для математического программирования, веб-сайт [33]), удобного решателя с мощным программным аппаратом, что очень важно для моделирования и решения реальных задач;

– анализ полученных численных результатов, их интерпретация, формирование списка практических выводов.

В настоящем исследовании используется модель линейного программирования, с помощью которой решается проблема оптимизации производства и логистики предприятия для достижения устойчивой работы предприятия при минимальных затратах. Модель построена на сетевой структуре, которая учитывает заводы, распределительные центры и доставку продукции клиентам. Потоки готовой продукции моделируются по всей цепочке поставок с явной детализацией затрат на производство, транспортировку готовой продукции и управление запасами. Модель включает в себя оптимизацию цепочки путем назначения количества распределяемой продукции для каждого района сети при соблюдении ряда ограничений, включающих: мощность заводов и распределительных центров, удовлетворение значений спроса по продуктам и по районам, баланс материальных потоков на заводах, баланс товарных потоков в распределительных центрах и условие неотрицательности переменных решений.

МАТЕРИАЛЫ И МЕТОДЫ

Постановка задачи. Компания, на которой основывалось исследование, относится к сектору массового потребления снеков. В настоящее время у нее есть два производственных предприятия, расположенных в Морозовске и Константиновске Ростовской области, на которых производятся различные линии продукции, распространяющиеся через торговые агентства в разных регионах страны. Оба завода имеют общее производство линии экструдированных продуктов, которые распространяются в основном в районы севера Ростовской области. Ассортимент: чипсы (пеллет), луковые колечки (пеллет), сухарики (пшенично-ржаные), арахис соленый, фисташки, семечки, кукурузные палочки, кукурузные колечки и др.

Структура затрат. В структуре затрат в цепочке поставок снеков можно выделить следующие компоненты [34][35]:

1. Стоимость приобретения или производства учитывает прямые или косвенные затраты на оплату труда, прямые или косвенные материальные затраты, общехозяйственные расходы (выраженные в денежной единице на единицу продукции).
2. Стоимость заказа. Административные и офисные расходы, связанные с процессом заказа на поставку, отправкой, обработкой заказа, транспортными расходами или стоимостью запуска партии продукции в случае производства (выраженные в денежной единице на заказ).
3. Стоимость хранения.Деньги, связанные с запасами, стоимость складских помещений, стоимость обработки, стоимость страхования, устаревание, ухудшение качества, стоимость ведения учета запасов (выраженные в денежной единице / единице измерения / единице времени).
4. Стоимость недопоставки/дефицита учитывает все потери, связанные с отсутствием товара или услуги: упущенная прибыль, затраты на экстренные закупки, штрафы за нарушение контрактов, потерю репутации и потенциальную потерю клиентов.
5. Типичная структура затрат на производство закусок состоит из сырья (MP), прямого труда (MOD), упаковочного материала (ME) и производственных накладных расходов (CIF). В CIF мы видим расходы на техническое обслуживание (Mtto), косвенную рабочую силу (MOI), коммунальные услуги, такие как вода, энергия, газ и другие, затраты на уборку, расходы на безопасность [36].

Инвентарь инкапсулирует деньги, и неправильное управление им может повлиять на финансовое положение компаний. Иметь слишком много запасов так же проблематично, как и слишком мало. Слишком много подразумевает ненужные дополнительные расходы, связанные с хранением, страхованием, налогами и теми, которые связаны с износом или устареванием товаров, которые хранятся на складе. Эти затраты растут с увеличением запасов. Однако есть и другие, которые уменьшаются при увеличении запасов.

Проблема, которую нужно решить. Каждая организация стремится к достижению и поддержанию конкурентоспособности, удовлетворению своих клиентов, минимизации своих затрат и увеличению прибыльности, для этого ей необходимы инструменты, позволяющие своевременно и адекватно принимать решения, направленные на снижение совокупных затрат, встречающихся в процессах закупки сырья, производства и распространения. Принятие этих решений становится трудным из-за размера и сложности компаний и большого количества переменных, с которыми они работают, особенно когда у них есть несколько продуктов, сырья, производственных предприятий и клиентов.

В рамках настоящего исследования предполагалось, что завод, находящийся в Морозовске, имеет ограниченную мощность. В настоящее время мощность этого завода составляет 113 215 коробок готовой продукции, 80 % которой реализуется в северных районах области. Мощность завода в Константиновске составляет 39 600 коробок в месяц. Средний спрос в месяц составляет 91 200 коробок.

Для компании жизненно важно знать эффект добавления затрат на производство, распределение, запасы, а также валовую прибыль, полученную для каждого из продуктов в соответствии с географическим положением клиентов. Необходимо определить, сколько, на каком заводе и каких продуктов необходимо производить, чтобы удовлетворить спрос потребителей, сводя к минимуму затраты, не забывая при этом о других факторах, таких как эффективность и мощность каждого из заводов.

Цель этой математической модели – ответить на поставленные вопросы, минимизировав соответствующие общие затраты и оптимизировав цепочку поставок. Анализ результатов будет включать, среди нескольких факторов, возможность инвестирования в завод в Морозовске для расширения его мощностей и, таким образом, повышения рентабельности производства без необходимости производства на заводе в Константиновске.

Вопросы можно сформулировать следующим образом:

– Какие и сколько продуктов должны быть произведены на каждом заводе?

– Какое распределение спроса должно быть у распределительных центров?

– Следует ли увеличить мощность заводов и как именно с учетом уровня эффективности и производительности каждого из производственных предприятий и географического положения районов?

Как уже было сказано, исследуемая компания имеет два производственных предприятия со следующими мощностями для расширенной линии:

Завод 1: Константиновск. Установленная мощность: 411 тонн в месяц. Используемая мощность: 66,4 %

Завод 2: Морозовск. Установленная мощность: 120 тонн в месяц. Используемая мощность: 98 %

Основным сырьем, поставляемым для этого процесса, является дробленая кукуруза, которая требует специальной обработки от помола до использования в производственном процессе. Эти два завода совместно производят ряд продуктов, которые в основном продаются в северных районах области. Расширенные продукты характеризуются малым объемом и, следовательно, оказывают большое влияние на издержки сбыта. Компания поставляет свою продукцию 11 торговых районов, среди которых: Белокалитвинский, Тацинский, Морозовский, Милютинский, Кашарский, Боковский, Шолоховский, Верхнедонской, Чертковский, Миллеровский, Тарасовский.

Система дистрибуции осуществляется из распределительных центров обоих заводов, с завода в Константиновске они отправляются в трех типах транспортных средств (грузовики до 3 тонн, 3–5 тонн и 5–10 тонн), а из Морозовска – только в грузовиках 3–5 тонн. В связи с тем что товары имеют очень низкое соотношение объем/вес, контракты на перевозку заключаются по маршруту, а не по весу. Согласно политике компании грузовик должен быть загружен более чем на 98 %, чтобы оптимизировать расходы.

Необходимо определить, сколько единиц каждого продукта должно производиться на каждом заводе каждый месяц и сколько единиц должно ежемесячно отгружаться с каждого склада в каждый район, чтобы минимизировать соответствующие общие затраты.

Поскольку стоимость запасов и складские мощности ограничены, необходимо ежемесячно отслеживать количество каждого продукта, хранящегося на каждом заводе. Следовательно, модель линейного программирования имеет три типа переменных решения: 1) объемы производства; 2) количество запасов; 3) отгруженное количество.

Компания управляет производственной системой в соответствии со своей технологической картой, которая начинается с проектирования и разработки продуктов. Когда продукты разработаны в соответствии с требованиями заказчика, запрос отправляется в процесс снабжения, который отвечает за управление поставками на каждый из заводов. Затем осуществляется производственный процесс по созданию продуктов, которые хранятся на складах, чтобы логистика распределения могла удовлетворить спрос коммерческого управления.

Сбор данных проводился внутри компании с помощью прямых интервью с участниками производственного процесса, в результате чего были сформулированы таблицы данных для модели (табл. 1, рис. 1).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Математическая модель и программная реализация

Математическая модель. Формула, установленная для определения общих затрат, была следующей:

CTR = Z×CPN + XY×CPN + XZ×CPN + +Z×CFI + XY×CF + XZ×CFE + Y×CINV,

где Z = количество единиц продукции, отправленных с завода на склад;

XY = количество единиц продукции, отправленных с завода в районы;

XZ = количество единиц продукции, отправленных со склада в районы;

Y = количество единиц продукции, хранящихся на складе;

CPN = стоимость производства единицы продукции;

CINV = стоимость хранения единицы продукции;

CFE = стоимость внешней перевозки единицы продукции;

CFI = стоимость внутренней перевозки единицы продукции;

CF = стоимость перевозки с завода в районы единицы продукции.

Общая стоимость производства продукции = XY×CPN + XZ×CPN.

Общая стоимость перевозки продукции = = Z×CFI + XY×CF + XZ×CFE.

Общая стоимость хранения продукции = = Y×CINV.

Структурирование математической модели. Данные, использованные в сценарии анализа, были собраны с учетом двух производственных предприятий. Специально были рассмотрены типы поставщиков по местонахождению и годовому объему, расположение складов и распределительных центров, транспортные расходы и постоянные затраты на складах.

Характеристики модели. Схематично модель можно представить так, как показано на рис. 2.

Общие характеристики моделируемой системы

Модель рассчитана на период планирования 7 месяцев.

Рассматриваются несколько продуктов.

В качестве переменной решения рассматривается количество продукции, которое должно быть произведено на каждом из заводов и распределено по каждому из районов.

Включены ограничения емкости, запасов и спроса.

Целевая функция включает в себя сумму всех затрат, связанных с цепью.

Районы могут получать продукты от любого из двух складов.

Не моделируются распределительные потоки от заводов к конечным потребителям.

Возможный переток продукции между заводами не предполагается.

Окончательный запас определяется для того, чтобы гарантировать поставку продукции и избежать ее отсутствия на складе.

Поскольку это скоропортящиеся продукты, учитывается срок их полезного использования.

Формулировка модели

Параметры и переменные для этой модели определяются с учетом затрат на хранение на складе, производственных затрат на заводах и фрахта, связанного с распределением.

Параметры

CAP_i = производственная мощность i-го завода;

CPN_ij = стоимость производства единицы j-го продукта на i-м заводе;

DEM_jkl = спрос на j-й продукт в k-м районе в течение месяца;

CINV_jm = стоимость хранения запасов j-го продукта в m-м распределительном центре;

CAPCEN_m = максимальная вместимость запасов m-го распределительного центра;

CFI_im = стоимость перевозки от i-го завода до m-го распределительного центра;

CF_ik = стоимость перевозки от i-го завода до k-го района;

CFE_mk = стоимость перевозки из m-го распределительного центра m-й район;

INVCEROC_jm = начальный запас j-го продукта j в m-м распределительном центре;

INFINAL_j = окончательная инвентаризация j-го продукта j в последнем месяце (декабрь).

Переменные решения

Y_jml = количество единиц j-го товара, хранящегося в m-м распределительном центре в течение месяца;

Z_jiml = количество единиц j-го товара, отгруженного из m-го распределительного центра в течение месяца;

XY_jlik = количество единиц j-го товара, отгруженного с i-го завода в течение месяца для k-го района;

XZ_zmlk = количество единиц j-го товара, отгруженного из m-го распределительного центра в течение месяца для k-го района.

Переменные решения представляют собой контролируемые переменные, которыми может управлять компания и которые прямо или косвенно решают задачу. В сформулированной модели компания может решить, сколько единиц продукции производить и отгружать на каждом из заводов, так же как будет происходить распределение потоков от склада к каждому из районов. Затем модель отвечает за поиск значений этих переменных, обеспечивающих минимальные общие затраты на производство, хранение и распространение.

Вербальная формулировка модели выглядит следующим образом:

Минимизировать: Общая стоимость производства + Стоимость запасов + Затраты на распространение.

Общая стоимость производства = количество произведенных коробок, помноженная на себестоимость единицы продукции.

Стоимость запасов = количество хранимых коробок, умноженное на стоимость единицы хранения.

Затраты на перевозку = количество отгруженных коробок, помноженное на стоимость перевозки за коробку.

Были определены следующие ограничения: мощность завода, удовлетворение спроса каждого района, максимальный запас, финальная инвентаризация, ограничения баланса, отправки.

Математическая модель в алгебраической записи

Ниже представлена целевая функция и ограничения в алгебраической записи.

Показанная целевая функция представляет собой сумму производственных затрат на каждом заводе (первая сумма), затрат на хранение запасов (вторая сумма), транспортных грузов от заводов до складов (третья сумма), грузов от заводов до районов (четвертая сумма), транспортные грузы из центров в районы (пятая сумма), себестоимость произведенных и отгруженных единиц (шестая сумма).

Ограничения

Ограничение производственной мощности. Сумма отгрузок продукции j с каждого завода i в районы m плюс продукция j, отправленная с заводов i в районы k, должна быть меньше или равна мощности каждого завода i.

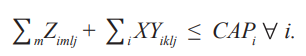
Удовлетворение спроса каждого района. Все поставки должны быть больше или равны потребности каждого района. Это ограничение означает, что количество единиц, отгруженных каждого продукта j из каждого распределительного центра m в каждый район k в месяце l, плюс количество единиц каждого продукта j, отгруженных с завода i в район k в каждом месяце l, должно быть больше или равно спросу каждого района k в месяц l на каждый продукт j.

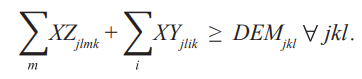
Максимальный запас. Общий запас всех единиц готовой продукции j, хранящихся в каждом распределительном центре, должен быть меньше или равен максимальной вместимости запасов каждого распределительного центра m.

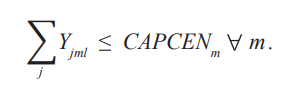
Окончательная инвентаризация. Запас каждого продукта на складе должен быть больше или равен окончательному определенному запасу.

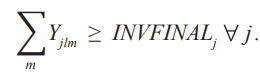
Остатки продукции в распределительных центрах:

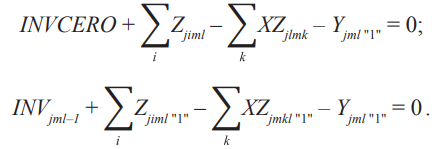
Ограничения указывают, что поток, поступающий на каждый склад со всех заводов, должен быть равен потоку, направляемому ко всем потребителям товара.

Отправка со склада. Все, что отправляется со склада во все районы K, должно быть, по крайней мере, тем, что было там в конце месяца (l-1). В конце месяца в распределительном центре не может храниться ни один продукт, которому больше месяца.

Отправка с завода. Минимальное количество коробок для отправки с заводов в районы – 600 штук. ОТПРАВКИ = 600 коробок.

Численная реализация модели в AMPL

В качестве инструментального средства для реализации проекта выбран язык AMPL как оптимальное по простоте использования, удобству и практичности программное обеспечение, позволяющее использовать готовые наборы решателей [37–40]. Решателями (solvers) называют алгоритмы для обработки моделей и чисел, которые вычисляют оптимальное решение.

AMPL – это язык для алгебраического моделирования и математического программирования: машиночитаемый язык для выражения задач оптимизации, таких как линейное программирование в алгебраической нотации.

AMPL включает в себя:

1. Язык моделирования – с помощью которого происходит описание и разработка математических моделей, данных оптимизации, переменных, целей и ограничений.
2. Командный язык – для просмотра моделей и анализа результато.
3. Язык сценариев – для сбора и обработки данных, а также для реализации различных схем исследований оптимизации.

Все языковые блоки AMPL используют одни и те же концепции и синтаксис для максимально упрощенного описания разрабатываемых сложных и комплексных моделей и приложений. Модель была запущена в интернете в NEOS-сервер, используя решатель Gurobi с входом AMPL. Был выбран набор решателей целочисленного линейного программирования GURIBI с линейными ограничениями. На сайте NEOS-сервер вводятся модель, данные и файл результатов, Программа выдает ответ за считаные секунды. На основе собранной информации была предложена планово-распределительная модель, позволяющая смоделировать текущую деятельность компании.

Командный файл и выходной файл в AMPL. Файл скрипта в AMPL используется, чтобы сообщить системе, как мы хотим, чтобы результаты были представлены, и какие из них мы хотим иметь на выходе. Для этой работы сценарий AMPL изображен на рис. 3.

Валидация модели

Валидация – это процесс проверки того, что результаты, предоставляемые моделью для выходных переменных и параметров, не сильно отличаются от результатов, измеренных в реальности.

Существуют различные индексы, которые позволяют количественно оценить степень соответствия между измеренными данными и результатами модели. Если модель построена правильно, можно провести анализ чувствительности, чтобы определить, какие параметры следует измерять с большей точностью и большим пространственным разрешением. В этом случае мы будем измерять изменчивость реальных данных, установленных компанией, по сравнению с данными ящиков, распределенных в предлагаемой модели. В следующей таблице приведены результаты, полученные в соответствии с фактическим распределением за январь – апрель, и данные, полученные при вводе этих фактических данных в модель.

Проверка состояла в том, чтобы взять реальные данные о единицах, отправленных в период с января по апрель этого года, и включить их в модель AMPL. Фактические значения были предоставлены компанией.

Результаты показывают (табл. 2), что существенных отличий от реальной модели нет. Что касается количества распределенных коробок, разница составляет 4 364 коробки, что представляет собой отклонение на 0,94 % по отношению к количеству, отправленному в течение установленных месяцев. В случае затрат представлены очень низкие вариации, коэффициент вариации составляет 0,66 %, что указывает на надежность модели выше 99 %.

Еще одним важным моментом для проверки модели является проверка того, что все ограничения полностью выполняются.

Производственная мощность. Производственная мощность определяется количеством коробок, отправленных с заводов в распределительные центры (Z) и с заводов в районы (XY). Эти количества зависят от текущей мощности каждого завода, поэтому сумма количества, отправляемого в распределительные центры и районы, не должна превышать эту мощность. Результаты показывают, что ограничение мощности выполнено.

Константиновск:

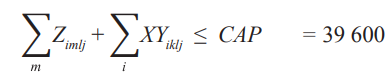
11 268 + 0 = 11 268 ≤ CAP .

Морозовск:

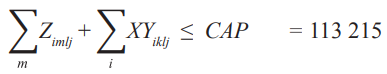
3 599 + 102 030 = 105 628 < CAP.

Запасы. Для запасов у нас есть два связанных ограничения. Первый установлен, чтобы не хранить больше, чем текущая вместимость распределительных центров, а второй определяется минимальным количеством единиц в соответствии с политикой инвентаризации.

Константиновск:

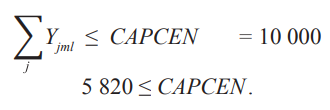
Морозовск:

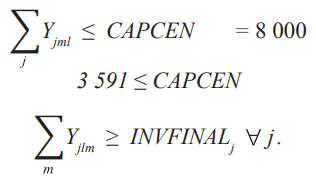
Спрос районов. Должен удовлетворяться единицами, отправляемыми с заводов (XY) и из распределительных центров (XZ).

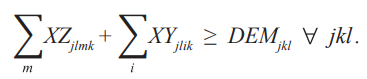
Средний спрос в период с января по апрель составил 116 056 коробок.

15 117 + 102 030 = 117 147 ≥ DEM_jkl .

Это соответствует ограничению спроса.

При текущем прогнозе на период с июня по декабрь, который составляет в среднем 91 274 ящика, мощности завода в Морозовске будет достаточно, чтобы удовлетворить спрос. Месяцем с самым высоким спросом является декабрь с 97 433 ящиками, что делает возможным производство на указанном заводе, чья текущая мощность составляет 113 215 ящиков.

Полученная целевая функция показала, что соответствующие общие затраты на эксплуатацию и распространение в течение семи исследуемых месяцев составляют: CTR (июнь – декабрь) = 7 601 578 720 (тыс. руб.).

Для оптимальной работы модель дает следующие результаты:

1. Производство: 99 % продуктов должно производиться на заводе в Морозовске.
2. Распределение: 92 % отгрузок должно осуществляется напрямую с завода в Морозовск в районы; 8 % отправок должно осуществляться через дистрибъютора.
3. Запасы: 99 % запасов управляются складом в Морозовске.

Таким образом, добьемся минимизации затрат на производственные процессы, запасы и дистрибуцию, оптимизируя ресурсы компании.

ЗАКЛЮЧЕНИЕ

Разработана математическая модель, позволяющая оптимизировать организационные процессы предприятия с дискретным производством, используя математический аппарат линейного программирования, а также его реализацию в виде готового программного решения на основе генератора AMPL, оптимального по простоте использования, удобству и практичности программного обеспечения, позволяющего использовать готовые наборы решателей.

Основным результатом исследования является моделирование производственной цепочки предприятия дискретного типа, включающей производство, транспортировку, хранение, распределение и доставку продукции потребителям, направленное на минимизацию производственных затрат при соблюдении технологических требований. Модель апробирована на производственной цепочке предприятия Ростовской области по производству снеков, имеющего два завода – в Морозовске и Константиновске – и поставляющего свою продукцию в 11 районов области. Построенная модель может быть положена в основу пользовательского программного комплекса, направленного на поддержку малого и среднего предпринимательства.